opredelitev enačbe
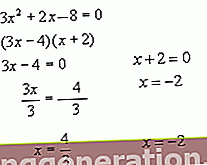V matematiki se enakost med dvema algebrskima izrazoma imenuje enačba, ki jo bomo imenovali člani enačbe. V enačbah bodo prikazani povezani z matematičnimi operacijami, številkami in črkami (neznanke).
Večina matematičnih problemov najde pogoje, izražene v obliki ene ali več enačb.
Ko bo katera koli vrednost spremenljivk v enačbi dosegla enakost, bo ta položaj imenovan rešitev enačbe.
Pred enačbo se lahko pojavijo naslednji scenariji, da nobena od vrednosti neznanega ne doseže enakosti ali nasprotno, da jo izpolnjuje vsa mogoča vrednost neznanega, v tem primeru bi se soočili s tistim, kar se imenuje identitete v matematika in ko se dva matematična izraza sovpadata v neenakosti, bo to določeno kot neenakost.
Obstajajo različne vrste enačb, med njimi najdemo funkcionalno enačbo, v kateri konstante in spremenljivke niso realna števila, temveč funkcije. Ko se v nekaterih članih pojavi diferencialni operator, jih imenujemo diferencialne enačbe. Potem je tu še polinomska enačba, ki bo tista, ki vzpostavi enakost med dvema polinoma. Po drugi strani so enačbe prve stopnje tiste, pri katerih spremenljivka x ni dvignjena na nobeno stopnjo, pri čemer je 1 njen eksponent. Medtem pa je značilnost in diferencialna značilnost enačb, znanih kot enačbe druge stopnje, ta, da bodo imeli dve možni rešitvi.
Toda za astronomijo, kjer izraz tudi pravi prisoten, je enačba razlika med krajem ali povprečnim gibanjem in resničnim ali navideznim, ki ga ima zvezda.
