opredelitev konkavnega
Konkavni izraz je izraz, ki se uporablja tako v matematiki (zlasti geometriji) kot v fiziki, da se nanaša na vrsto kota, ki je ustvarjen pred krivuljo in zavzame notranjo stran le-te, torej tam, kjer nastaja notranja votlina. . Nasprotno od konkave je konveksni izraz, zunanja stran krivulje. Oba izraza se običajno uporabljata kot kvalificirana pridevnika in se lahko uporabljata za označevanje različnih elementov ali predmetov, v katerih se pojav pojavlja.
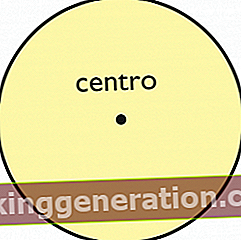
Etimologija besede konkavno ni povsem jasna, ker čeprav se trdi, da lahko izhaja iz latinskega izraza kavus ali votlino, je tudi verjel, da je grški izraz kutos dalo bi votlino. Ideja konkavnega koncepta je navsezadnje in ne glede na njegov izvor prisotnost votline, ki postane vidna, ko ravna črta postane krivulja, ki ločuje prostor na dve polravnini: eno notranjo in eno zunanjo krivulji .
Ko govorimo o notranji ravnini krivulje, mislimo na tisto ravnino, ki je krivulja skoraj zaprta, medtem ko bo zunanja tista, ki jo predstavlja vse zunaj. Tako se bo notranja ravnina preoblikovala v konkavno ravnino, ker ker krivulja ni ravna črta, bo med ravninama nastalo neravnovesje in ena bo imela votlino, druga pa bo predstavljala ukrivljenost nasprotne strani . V tem smislu je pomembno opozoriti, da beseda konveksno izhaja iz latinščine in pomeni Nosi na hrbtu, s čimer se razume, da beseda predstavlja stran, ki se zdi upognjena od obeh, ki lahko ustvarita krivuljo.
Tako teoretični kot abstraktni koncepti so uporabni za resničnost v mnogih objektih, pri katerih opazimo ukrivljenost in nastanek teh dveh ravnin, na primer konkavno stran leče.
